# Author's write-up for FlagHash A quick history: I wasn't originally writing for vsctf or anything. But Quasar and I were having a discussion about a paper called [Practical Cryptanalysis of SFLASH](https://eprint.iacr.org/2007/141.pdf), and in particular the bilinear differential introduced in the paper. In trying to extract the core mathematics of the paper, I think we removed so much of the SFLASH protocol that the challenge no longer looks anything like it, but I think it's a fun paper regardless and you can probably see how it inspired the challenge. To that end I'd like to say we co-wrote this challenge, but Quasar also says I did this all by myself, so here we are. <details> <summary>Challenge code</summary> ```python= import string flag = open('flag.txt').read().strip().encode() F = GF(127^29, 'x', modulus=list(flag)) FlagHash = lambda s: bytes((F(list(s.encode()))^128).polynomial()[:20]).hex() for _ in range(1337): s = ''.join(sample(string.ascii_letters + string.digits, randint(13,37))) print(s, FlagHash(s)) ``` </details> The hash itself isn't too complicated, it takes a finite field of order $127^{29}$ but whose modulus is unknown (and is in fact the flag itself). You convert your string `s` into an element of this field, calculate its 128th power, and the resulting polynomial is the hash. Oh, except it's truncated to the first 20 coefficients, so the last 9 coefficients are deleted. ## Part 1: Recovering the forward map First thing to note is that the map $f: w \mapsto w^{128}$ is quadratic, since $w \mapsto w^{127}$ is just the linear Frobenius map. That means that $f$ can be represented as a series of 29x29 matrices, one for each coefficient of its output. Specifically, if $w = (w_1, w_2, \ldots, w_{29})$, then there exists symmetric matrices $M_1, M_2, \ldots, M_{29}$ such that $w^{128} = (wM_1w, wM_2w, \ldots, wM_{29}w)$, where we've abused the notation so that $w^{128}$ is also a vector. Our hash map $h$ is then just the projection of $f$ to the first 20 elements. Knowing this, we can recover $M_1$ to $M_{20}$ fairly easily, since each one only has $\binom{30}{2} = 435$ degrees of freedom. ```python= hashes = [line.split() for line in open('output.txt','r').readlines()] s2v = lambda s: list(s.encode().ljust(29, b'\0')) vs = [(s2v(s), s2v(bytes.fromhex(h).decode())[:20]) for s,h in hashes if len(s) <= 29] mat = matrix(GF(127), [[x*y for x in v_in for y in v_in] + v_out for v_in, v_out in vs]) soln = mat[:,:841].solve_right(mat[:,841:]) ``` These matrices fully determines our map, so we can now hash any string we want (as long as it's no longer than 29 characters). We can probably extend this to 37 using the longer strings, but this is not necessary. ## Part 2: Recovering first 20 bytes of flag Even though we have the above, it turns out that these coefficients themselves already give very good information. Let's look at the first five rows, say, via `print(soln[:5])`. This prints out the first five elements ``` [ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 37 89 83 121 2 50 93 14 75 68 108 32 52 58 53 30 65 102 103 33] [108 3 88 52 51 88 10 118 109 106 37 94 55 88 54 74 24 85 39 54] [ 1 66 18 100 90 102 44 116 57 23 9 4 56 73 6 31 31 87 74 6] [ 14 59 74 30 121 50 0 20 45 11 37 47 31 96 99 124 32 63 18 54] ``` Now, I've cheated a bit so $M_1$ as I've described above is really the first column, and also is not actually symmetric, but it doesn't matter too much. These rows correspond to the (first 20 coefficients of the) polynomials: 1) $x^0$ 2) $x^1 + x^{127}$ 3) $x^2 + x^{254}$ 4) $x^3 + x^{381}$ 5) $x^4 + x^{508}$. In fact, for any $0 \leq i,j \leq 29$, we can get $x^{127i+j} + x^{127j+i}$ directly as a row of this matrix. So let's first have a look at $x^{127}$ and $x^{128}$. ```python= x127 = soln[1] - vector([i==1 for i in range(20)]) x128 = soln[30] print(f'{x127 = }') print(f'{x128 = }') # x127 = (37, 88, 83, 121, 2, 50, 93, 14, 75, 68, 108, 32, 52, 58, 53, 30, 65, 102, 103, 33) # x128 = (66, 125, 124, 79, 8, 116, 64, 63, 56, 124, 91, 65, 125, 2, 15, 76, 22, 26, 125, 87) ``` Here's an image of it, showing in particular where all the unknown (blanks) are. We'll explain in a bit how the `70` at the end can be determined.  One thing we can do here is that $x^{128}$ is just $x^{127}x$, so this is just shifting the first vector right by 1, and then multiply the rightmost value (which we pop off from the vector) by the modulus. In other words, the modulus must be a multiple of $(66-0, 125-37, 124-88, \ldots)$. Since we also know the flag begins with a `'v'`, we can scale it accordingly: ```python= first20 = x128 - vector([0]+list(x127)[:-1]) first20 *= ord('v') / first20[0] first20 = bytes(first20) print(f'{first20 = }') # first20 = b'vsctf{fl4g_ha5h_is_S' ``` And we have the first 20 bytes of the flag! To work out the value at the end of $x^{127}$ as we had before, we just need to figure out how much this vector was multiplied by, since we know the first and last bytes of the modulus. ```python -mod(66,127) * ord('}') / ord('v') ``` which gives us the 70 at the end. This isn't particularly useful here, but it does chain into the next part! ## Part 3: Recovering the last 9 bytes Ok, so we can already do quite a few things, but turns out that last 9 bytes is much harder than everything so far. This is because you need to know something above and below in order to get some information out of it. Or with the shifting notion we had, we can link a coefficient to a coefficient to its bottom-right. In that case, we can actually bridge a gap of size 9 by having 19 consecutive powers. For the purpose of this solution, I will use $x^{127\times18} = x^{2286}$ and $x^{128\times18} = x^{2304}$ because those are readily available. But with a bit more effort you could also use, say, $x^{127}$ and $x^{145}$ or similar. Anyway, for our case of 2286 and 2304, we don't readily have everything in between, but it's quite easy to interpolate since we know that the difference is a linear sum of shifts of the modulus. ```python= x2286 = soln[18] - vector([i==18 for i in range(20)]) x2304 = soln[30*18] print(f'{x2286 = }') print(f'{x2304 = }') # x2286 = (23, 112, 120, 3, 4, 72, 80, 57, 124, 88, 84, 122, 71, 28, 110, 96, 122, 3, 12, 105) # x2304 = (44, 54, 26, 29, 27, 99, 44, 41, 87, 118, 13, 89, 3, 22, 1, 31, 66, 10, 57, 24) ``` We can do this as before, learning not only all values in between but also the last coefficient.  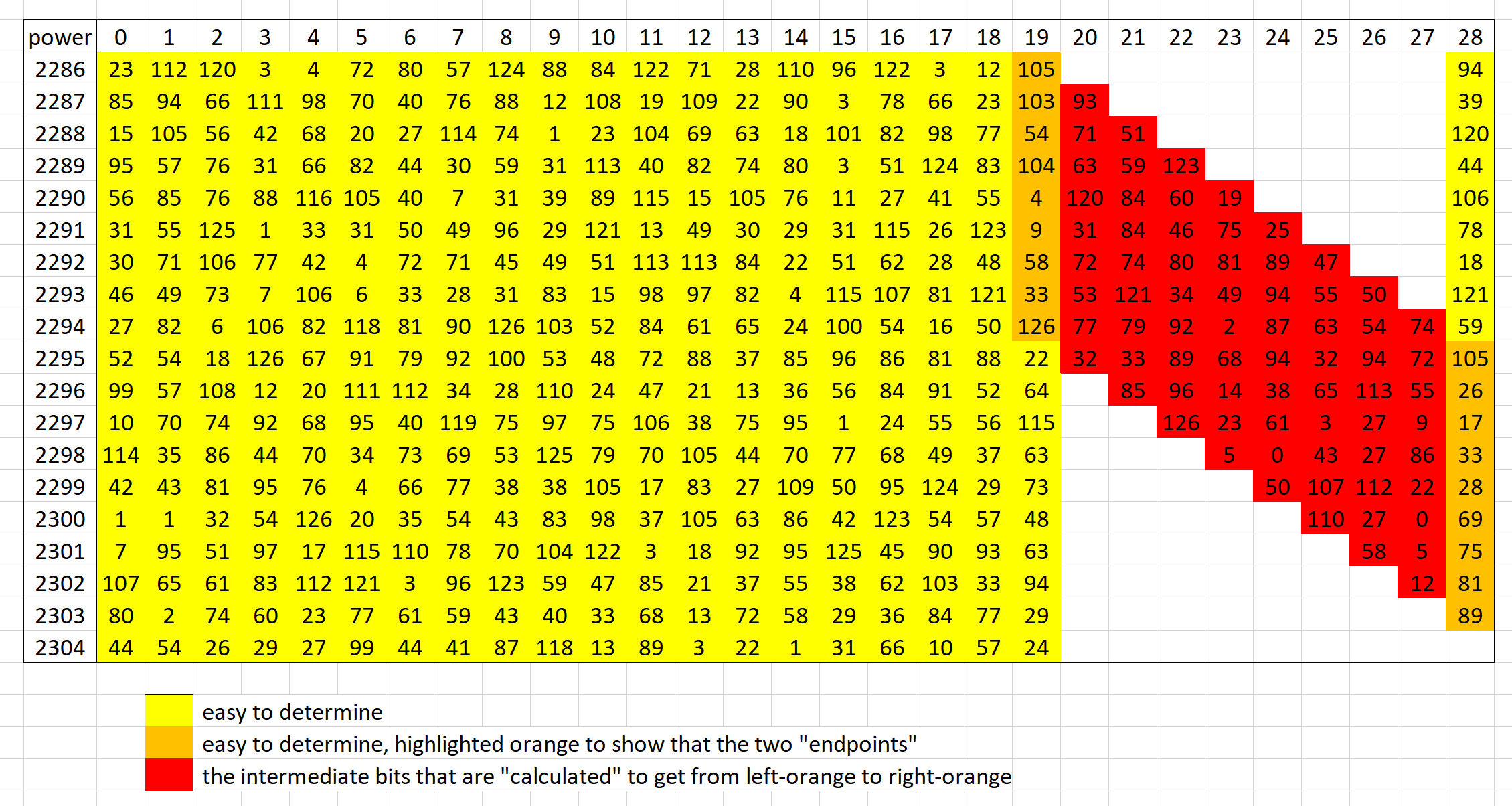The gap of length 9 then represents the unknown parts of our modulus, but by chaining them this way, we see that it's really just a system of linear equations. We have 9 equations with 9 unknowns, and thus we can solve the modulus. (We don't need to solve all the intermediate red values, it's really just there for demonstration.) ## Putting it all together Here's the combined solve script: ```python= hashes = [line.split() for line in open('output.txt','r').readlines()] s2v = lambda s: list(s.encode().ljust(29, b'\0')) vs = [(s2v(s), s2v(bytes.fromhex(h).decode())[:20]) for s,h in hashes if len(s) <= 29] mat = matrix(GF(127), [[x*y for x in v_in for y in v_in] + v_out for v_in, v_out in vs]) soln = mat[:,:841].solve_right(mat[:,841:]) #print(soln[:5]) x127 = soln[1] - vector([i==1 for i in range(20)]) x128 = soln[30] print(f'{x127 = }') print(f'{x128 = }') first20 = x128 - vector([0]+list(x127)[:-1]) first20 *= ord('v') / first20[0] first20 = bytes(first20) print(f'{first20 = }') x2286 = soln[18] - vector([i==18 for i in range(20)]) x2304 = soln[30*18] print(f'{x2286 = }') print(f'{x2304 = }') tmp = x2304 - vector([0]*18+list(x2286)[:-18]) arr = [] zz = first20 for _ in range(18): arr.append(zz) zz = bytes(1) + zz[:-1] muls = matrix(arr).solve_left(tmp)[::-1] target = (muls * 2)[9:] target init = x2286[-9:] for i in range(8): init += vector(GF(127), first20[i-8:] + bytes(i+1)) * muls[i] init = init[::-1] print(init) print(target) mat = matrix.hankel(muls[:9], muls[9:-1]) last20 = bytes(mat.solve_right(target-init)) print(first20 + last20 + b'}') ``` which prints out the following ``` x127 = (37, 88, 83, 121, 2, 50, 93, 14, 75, 68, 108, 32, 52, 58, 53, 30, 65, 102, 103, 33) x128 = (66, 125, 124, 79, 8, 116, 64, 63, 56, 124, 91, 65, 125, 2, 15, 76, 22, 26, 125, 87) first20 = b'vsctf{fl4g_ha5h_is_S' x2286 = (23, 112, 120, 3, 4, 72, 80, 57, 124, 88, 84, 122, 71, 28, 110, 96, 122, 3, 12, 105) x2304 = (44, 54, 26, 29, 27, 99, 44, 41, 87, 118, 13, 89, 3, 22, 1, 31, 66, 10, 57, 24) (105, 103, 54, 104, 4, 9, 58, 33, 126) (105, 26, 17, 33, 28, 69, 75, 81, 89) b'vsctf{fl4g_ha5h_is_SFL45H_UwU}' ``` The flag is `vsctf{fl4g_ha5h_is_SFL45H_UwU}`.